Bret Alexander Beheim

Missing data, moralizing gods, and the siren song of Aeiea

Update 2021-07-07: I’ve revised some sections of this piece based on developments since it was originally published. In particular, the original paper has been retracted by the authors.

Missing data is probably the most under-trained topic in data analysis. Methods courses prepare students for performing all kinds of robustness checks on data they have, but what to do when some of your data is missing is relegated as special topics, or left for higher-level courses.

This is a mistake, I think, because missingness is a ubiquitous problem, as are ad hoc solutions like the following entirely hypothetical methods section:

Our study has presence/absence data for some phenomenon, but some of the data points are missing. Since we are really just interested in whether the phenomenon is present, we redefine both “phenomenon absent” and “data unknown” to “phenomenon not known to be present”, solving the missing data problem.

This error appears so often it’s proverbial: the mistake of assuming absence of evidence is evidence of absence, or AEIEA.

This is on my mind because of a high-profile paper this year on the first appearance of morality in world religion by the Seshat historical research team. The authors, led by Oxford anthropologist Harvey Whitehouse, argue that moral concepts like karma or the supernatural punishment of cheaters appear very recently in history, and mostly in societies larger than a million people.

Figure 1. A statue of Aeiea, goddess of missing data (at least, pending evidence to the contrary)

If true, this would be a big result. Looking carefully at the authors’ raw data, however, we find an massive problem - nearly 2/3rds of their “moralizing gods” measure (61%) are actually missing values.

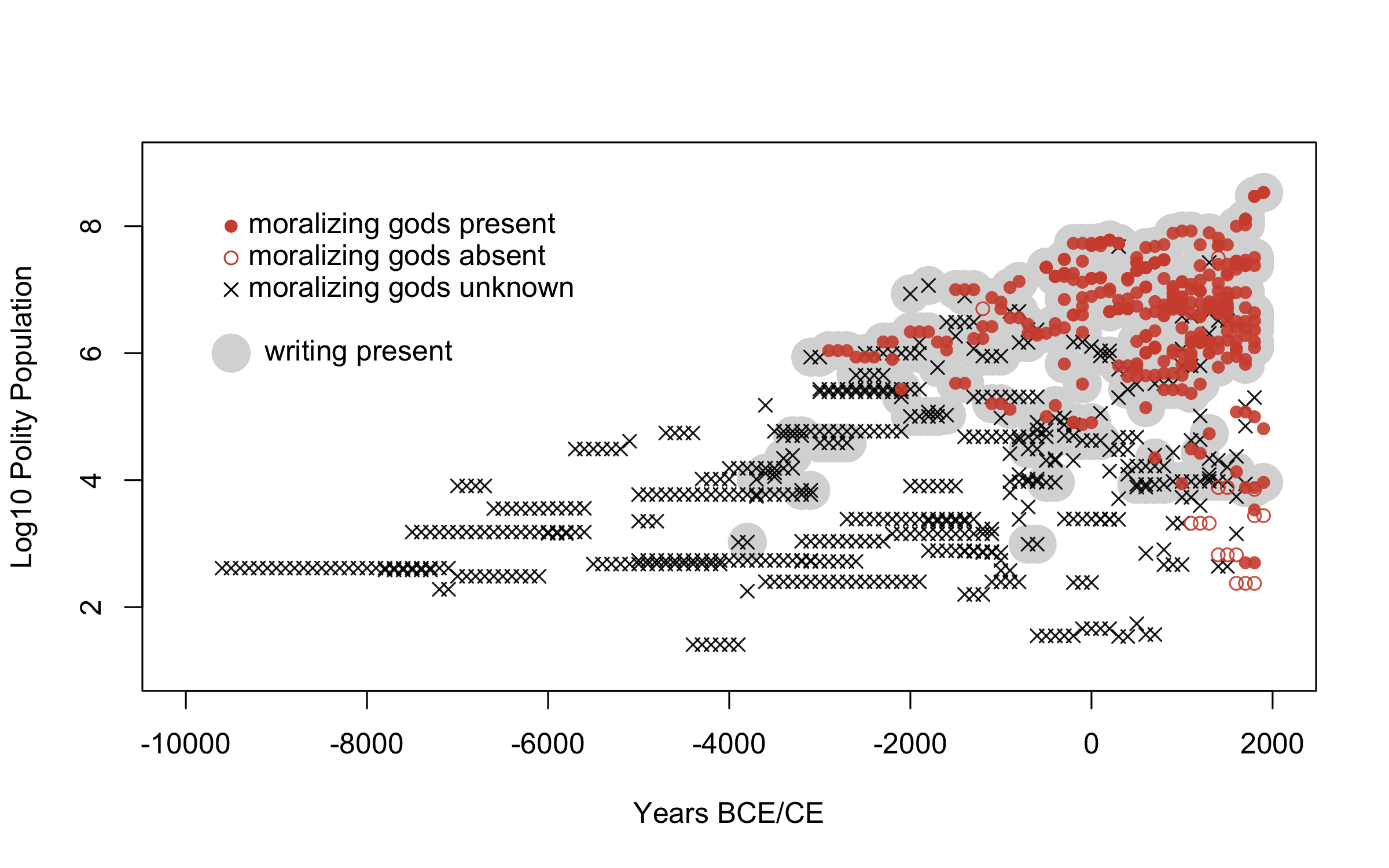
Figure 2. Reanalysis of Seshat data from Beheim, et al. (2019); visualization with Richard McElreath

So much data is missing about supernatural morality across time because such beliefs naturally require written evidence. This is probably an insurmountable problem, but in an analysis they describe as “far beyond the state of the art”, the Seshat team developed a workaround: assume AEIEA, and recode all missing values to “not known present”.

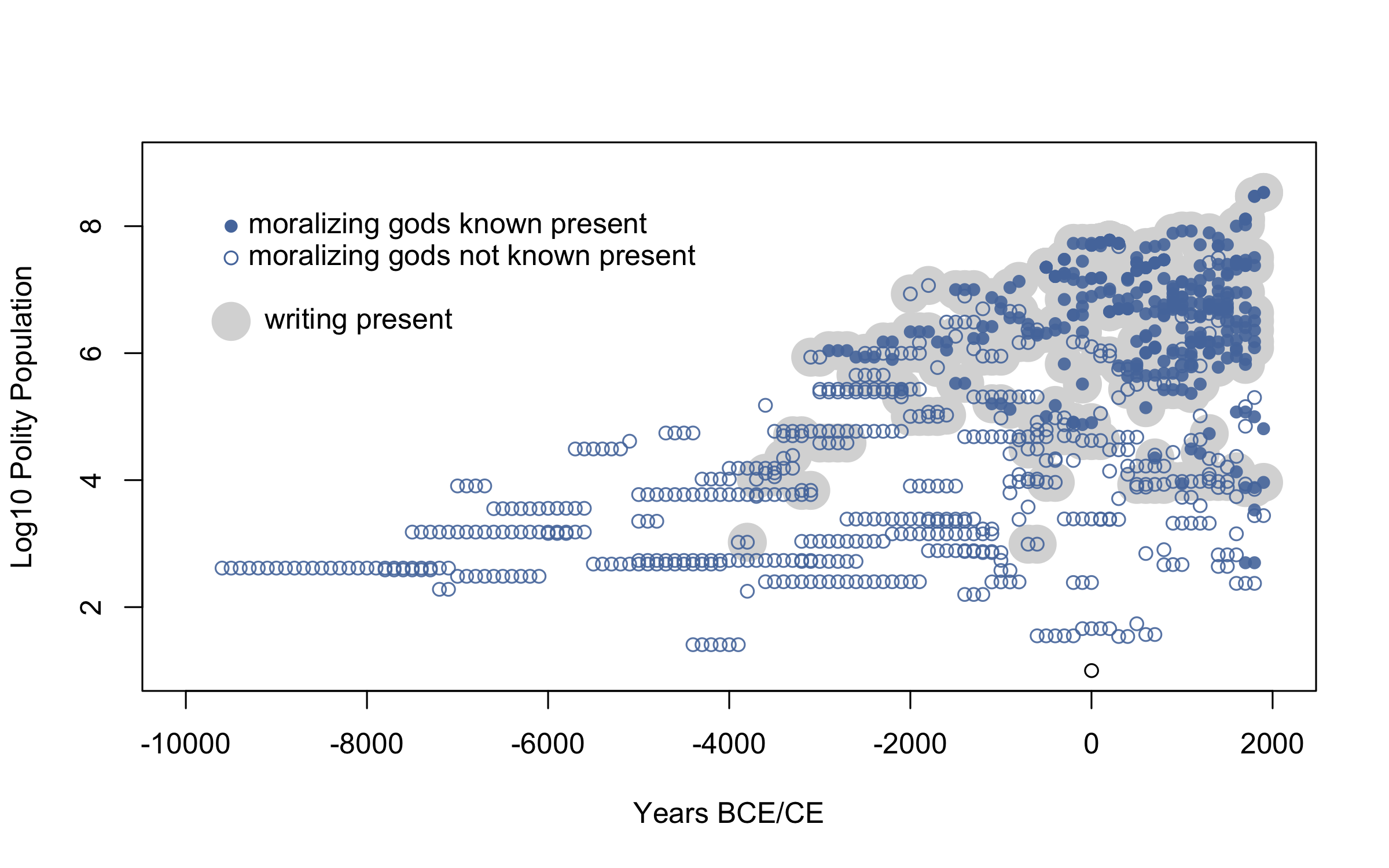
Figure 3. The ‘moralizing gods’ outcome variable as it was used in the statistical analyses of Whitehouse, et al. (2019)

Voila! The missing values have been reasoned into data points. This fateful assumption was never described in the published manuscript, and since most of the actual data comes from large, literate populations, and moralizing gods are present everywhere in this sample, their key findings immediately result from applying AEIEA.

This seems like statistical malpractice, but is it really that bad? Data imputation, e.g. using the mice package in R, also fills in missing values. And, the coding “not known to be present” really does cover both “unknown” and “known to be absent” logically. So what’s wrong?

To see the AEIEA fallacy, imagine that each data point in Figure 2 represents a pill that is either deadly poison, 🔴, or life-saving medicine, ⭕. You were only able to test 39% of the pills in the sample, finding almost all poison 🔴, while the remainder are untested, $\times$. I don’t think anyone - including the authors of the moralizing gods paper - would be happy to relabel the untested pills “not known to be poison” and eat them.

This demonstrates how the AEIEA assumption is invalid, but specific examples are inadequate to combat such a seductive fallacy. AEIEA is something like a cognitive attractor, with its seemingly-correct reasoning and almost magical ability to ‘solve’ missingness problems. Also, under certain circumstances, it actually is valid. So, it’s not enough to quote proverbs at people; we need to explain why AEIEA is a fallacy.

For any particular observation of the phenomenon of interest, let’s distinguish two events. First, we define whether the phenomenon really is present in the study system, $x$, or absent, $!x$. Separately, we can also define the event that outcome data is known in our dataset, $d$, or is unknown, $!d$. Our goal is then to estimate the true rate of occurrence across observations, the probability $p(x)$, given that $p(d) > 0$ and some information is incomplete.1

Expressed in the language of probability theory, the AEIEA assumption is

$$ p(x\vert !d) = 0. $$

Read literally, this says that conditioning on the outcome being unknown in our dataset, $p(\cdot \vert !d)$, conveys the same information about the phenomenon as learning the phenomenon was actually absent, i.e. $p(x\vert !x) = 0$.2 Plugging the AEIEA assumption into the law of total probability,

$$ p(x) = p(x\vert d) p(d) + p(x\vert !d) p(!d), $$

it follows that,

$$ p(x\vert d) = p(x) / p(d). $$

Under AEIEA, the data we observe is thus dependent with the missingness distribution, since $p(x\vert d) > p(x)$.3 If we apply Bayes’ rule to the left-hand side of the previous equation, we have

$$ p(d\vert x) p(x) / p(d) = p(x) / p(d), $$

which simplifies to

$$ p(d\vert x) = 1. $$

We have proven something that, at least to me, was not immediately obvious: assuming AEIEA also assumes that if the phenomenon is actually present, it must have been recorded as such in our dataset. Or, equivalently, it cannot become missing data.

Thus, AEIEA is an extreme assumption about the relationship between $x$ and $d$ because it requires strong claims about the nature of missingness.4 If even a few poison pills are in the untested group in the example above, assuming AEIEA would be deadly.

This is not to say that AEIEA is always wrong, however. AEIEA really does work when, for example, the study system only has a finite number of “hits”, and you’ve already found them all. This is true in simple games like Minesweeper, Blackjack or Battleship. Here, we have a clear theory (the game rules) about the relationship between $x$ and $d$ which explains why the data cannot ever become missing when the phenomenon is present.

Figure 4. In Battleship, if you know where all the enemy ships are, absence of data on a cell is equivalent to knowing it is empty - AEIEA is valid.

Determining the validity of AEIEA is thus a scientific problem, not a statistical one, and the probabilistic conditions above help us understand what the scientific theory has to show. In the case of the unknown moralizing gods data all becoming absences, we’d need relatively fantastical theories about data preservation for AEIEA to work. If a South American jaguar figurine or Hawaiian ancestral family god was ever imbued with moralistic authority, then we must explain how those events have to survive into the historical records of today in order to conclude a lack of evidence actually means it never happened. Since such theories are not forthcoming in real datasets of religion, AEIEA is a fallacy.

This all may seem obvious, but the siren song of AEIEA is powerful and can easily lure unwary, but otherwise meticulous, researchers. For this reason, the astronomer and science popularizer Carl Sagan included AEIEA as part of his “baloney detection kit” of the common tools charlatans and cranks use to promote pseudoscience. Sagan even satirized AEIEA’s misuse in the study of human morality extended to a galactic scale, writing,

There may be seventy kazillion other worlds, but not one is known to have the moral advancement of the Earth, so we’re still central to the Universe.5

References:

R scripts for Figures 2 and 3:

library(rethinking)

# data from step 06_prep_regression_data
# at https://github.com/babeheim/moralizing-gods-reanalysis
d <- read.csv("./RegrDat.csv", stringsAsFactors = FALSE)

png("missing.png", height = 5, width = 8, res = 300, units = "in")

plot(1, 1, type = "n", xlim = c(-10000, 2000), ylim = c(1, 9),
  xlab = "Years BCE/CE", ylab = "Log10 Polity Population")

tar <- which(d$Writing == 1)
points(d$Time[tar], d$PolPop[tar], pch = 16, col = gray(0.85), cex = 3)

tar <- which(d$MG_missing == 1)
points(d$Time[tar], d$PolPop[tar], pch = 4, col = col.alpha("black", 0.9))

tar <- which(d$MG_missing == 0)
points(d$Time[tar], d$PolPop[tar], pch = ifelse(d$MG[tar] == 1, 16, 1), col = col.alpha("#D1523B", 0.9))

points(-9500, 8, pch = 16, col = "#D1523B")
text(-9500, 8, pos = 4, label = "moralizing gods present")
points(-9500, 7.5, pch = 1, col = "#D1523B")
text(-9500, 7.5, pos = 4, label = "moralizing gods absent")
points(-9500, 7, pch = 4, col = "black")
text(-9500, 7, pos = 4, label = "moralizing gods unknown")

points(-9500, 6, pch = 16, col = gray(0.85), cex = 3)
text(-9500, 6, pos = 4, label = "  writing present")

dev.off()

png("missing_to_0.png", height = 5, width = 8, res = 300, units = "in")

plot(1, 1, xlim = c(-10000, 2000), ylim = c(1, 9),
  xlab = "Years BCE/CE", ylab = "Log10 Polity Population")

tar <- which(d$Writing == 1)
points(d$Time[tar], d$PolPop[tar], pch = 16, col = gray(0.85), cex = 3)

points(d$Time, d$PolPop, pch = ifelse(d$MG == 1, 16, 1), col = col.alpha("#5679AB", 0.9))

points(-9500, 8, pch = 16, col = "#5679AB")
text(-9500, 8, pos = 4, label = "moralizing gods known present")
points(-9500, 7.5, pch = 1, col = "#5679AB")
text(-9500, 7.5, pos = 4, label = "moralizing gods not known present")

points(-9500, 6.5, pch = 16, col = gray(0.85), cex = 3)
text(-9500, 6.5, pos = 4, label = "  writing present")

dev.off()

Endnotes:

  1. The chance that the observation occurs, $d$, but is mis-coded from the true state, $x$ or $!x$, is important but distinct from the missing data problem. We here assume that either the phenomenon recorded accurately or is unknown. ↩︎

  2. This can get very confusing, as $p(x\vert !d)$ is the probability of $x$ given that the outcome is unknown in our data, while $p(x)$ is the probability of $x$ not knowing whether the outcome is known or unknown in our data. ↩︎

  3. Not all is lost though, since under AEIEA we can approximate $p(x)$ with the product of two quantities we can observe: $p(x\vert d) p(d)$. Further, if $p(x\vert d) \approx 1$ as in the moralizing gods dataset, then $p(x) \approx p(d).$ Given these assumptions about $p(x\vert d)$ and $p(x\vert !d)$, we don’t actually need to look at the presence/absence data! We simply need to know if any data was observed, and that approximates our target $p(x)$ extremely well. ↩︎

  4. The assumption used by Whitehouse, et al. (2019) is in fact the strongest possible version of the AEIEA fallacy, because $!d$ conveys complete information about $x$. A generalized AEIEA assumption is that $p(x\vert !d) < p(x)$, so conditioning on $d$ gives only partial information about the phenomenon’s occurrence. By the same logic as above, this implies that $p(d\vert x) > p(d)$, so the weak form of AEIEA assumes that conditioning on the phenomenon’s presence somehow increases the chances the data was recorded. In other words, similar theoretical requirements exist in the general AEIEA case as in the strongest version. ↩︎

  5. Sagan (1996), p.213 ↩︎